Waarom en hoe digitale filters gebruiken voor hoge-resolutie, hoge-snelheid, analoog-naar-digitaal omzettingen

Het is nog steeds een analoge wereld, maar digitale elektronica is alomtegenwoordig, en niet voor niets. Hoewel digitaal verschillende problemen oplost met algoritmische benaderingen, hebben zelfs de beste digitale algoritmen tekortkomingen bij het omgaan met entiteiten uit de echte wereld die in het analoge domein bestaan. Dit is vooral het geval bij toepassingen die gegevensverwerving met hoge snelheid en hoge resolutie vereisen, zoals instrumentatie, motorbesturing en systemen voor gegevensverwerving.

Het probleem voor ontwerpers die dergelijke signalen uit de werkelijkheid willen opvangen en verwerken, is dat zij zo snel mogelijk naar het digitale domein moeten overgaan zonder de informatie van dat signaal aan te tasten. De oplossing komt van een eenvoudig middelingsalgoritme (om ruis te verminderen) met een analoge laagdoorlaatfilter (LPF) aan de voorzijde. Met deze technieken kan een geschikt toestel conversie met hoge resolutie en hoge snelheid bieden, met onboard analoge en digitale filtering.

Dit artikel bespreekt in het kort de problemen die gepaard gaan met het bereiken van hoge-resolutie, hoge-snelheidsconversies met een successive approximation register (SAR) analoog-digitaal-omzetter (ADC) die gebruik maakt van een analoge LPF en een gemiddeld digitaal filter, en waarom deze filtercombinatie een goede optie is voor de meeste toepassingen. Vervolgens wordt de Analog Devices AD7606C-18 achtkanaals SAR ADC geïntroduceerd en wordt getoond hoe te profiteren van de 1 megasample/s (MSPS) conversiesnelheid, de gelijktijdige bemonsteringsconvertorreeks en flexibele digitale filterfuncties.

Om te laten zien hoe de beste algemene prestaties kunnen worden bereikt, wordt in dit artikel de AD7606C-18 gecombineerd met de ADR4525 ultralage ruis, hoge nauwkeurigheid spanningsreferentie, ook van Analog Devices, om de benodigde SAR-nauwkeurigheid voor 18-bit conversies te verbeteren.

Analoge versus digitale filters

Als een analoog ingenieur en een digitaal ingenieur filters bespreken, kan de digitaal ingenieur analoog verwerpen. Dit zou een vergissing zijn. De filternorm bij elke analoog-digitaal (A/D) conversie is dat het analoge LPF vóór het digitale filter komt (Afbeelding 1).

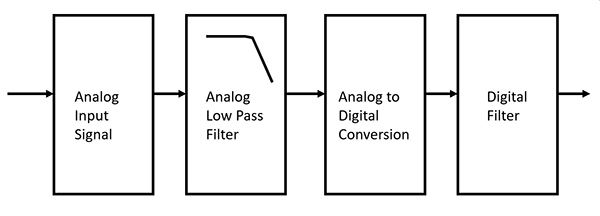Afbeelding 1: Een blokschema van een analoog-digitaal signaalketen met het analoge filter vóór het digitale filter. (Bron afbeelding: DigiKey)

Nadat de analoge LPF de hogere frequenties boven de gewenste bandbreedte heeft verzwakt, zet de ADC het signaal om in een digitaal woord. Na deze voltooiing kan het digitale filter op het signaal werken binnen de gewenste bandbreedte.

Analoge filters in data-acquisitieomgevingen

Het belang van de analoge LPF komt aan het licht bij de uitgang van de ADC. Elk signaal dat door de ADC gaat, heeft een bijbehorende magnitude en frequentie. Aan de uitgang van de ADC blijft de grootte van het signaal op betrouwbare wijze gelijk als de signaalfrequentie onder de ingangsbandbreedte van de ADC ligt. Hoewel de A/D-omzetting de signaalmagnitude behoudt, geldt dit niet voor de frequenties van het signaal. Men kan een verandering waarnemen in de frequenties boven ½ van de bemonsteringsfrequentie van de ADC, f_S, ook bekend als de Nyquist-bemonsteringsfrequentie (Afbeelding 2).

Afbeelding 2: In grafiek (A) heeft de fast Fourier transformweergave (FFT) van een ingangssignaal vijf frequentiecomponenten. Na een A/D-conversie toont de FFT-weergave in grafiek (B) alle vijf signalen die onder de helft van de bemonsteringsfrequentie (f_S) van de ADC voorkomen. (Bron afbeelding: DigiKey)

In Afbeelding 2 wordt in beide FFT-plots gebruik gemaakt van een logaritmische frequentie op de x-as en een lineaire spanning of magnitude op de y-as. In grafiek (A) toont de FFT-weergave van het analoge signaal het ingangssignaal van een ADC met meerdere signalen of ruis boven de helft van de ADC-bemonsteringsfrequentie, of f_S/2.

Bij vergelijking van deze twee grafieken is het nuttig de vijf FFT-signalen te volgen. Na een ADC-conversie blijven de grootheden van het oorspronkelijke signaal gelijk, maar de frequenties boven de helft van de bemonsteringsfrequentie in (A) worden "omgedraaid" terug onder f_S/2 in (B). Dit verschijnsel staat bekend als signaal aliasing. Om het signaal nauwkeurig te verwerven, moet de bemonsteringssnelheid f_S van de ADC groter zijn dan twee maal f_MAX, waarbij f_MAX gelijk is aan de bruikbare bandbreedte van het signaal, volgens de Shannon-Nyquist-bemonsteringstheorema.

Men kan zien hoe ADC's permanent ongewenste ruis en signalen in het digitale uitgangssignaal implanteren. Deze verandering maakt het onmogelijk om aan de uitgang van de convertor het verschil te zien tussen in-band signalen en out-of-band signalen.

Men zou kunnen verwachten dat er een pad heen en weer is tussen deze twee FFT-representaties. Maar als deze transformatie eenmaal heeft plaatsgevonden, is er geen weg terug om het ongedaan te maken. Helaas ondersteunt de wiskunde dit soort heen en weer gaan niet.

Terug naar het analoge/digitale debat: een digitaal filter is ongetwijfeld in staat middeling, eindige impulsrespons (FIR) of oneindige impulsrespons (IIR) filtering toe te passen, en daardoor de systeemruis te verminderen. Elk digitaal filter vereist echter een aanzienlijke hoeveelheid oversampling (het proces waarbij een signaal wordt bemonsterd met een bemonsteringsfrequentie die aanzienlijk hoger ligt dan de uiteindelijke datasnelheid van de uitgang), hetgeen tijd en energie kost en de bemonsteringssnelheid van de ADC verlaagt. Het digitale filter en de convertorfunctie kunnen de verschijnselen van het signaal met aliassen niet ondervangen. Het is het beste om de ruis van hogere frequenties eenvoudigweg vanaf het begin te verminderen, zelfs met een rudimentaire analoge LPF van de eerste orde.

Gemiddelde van digitale filters

SAR ADC's verbeteren hun DC-ruismeting met een gemiddeld digitaal filter. Het digitale filter met middeling verwerft meerdere omzettingen met een consistente tijdschaal om het aantal bits te verhogen. ADC-gebruikers gebruiken middelingsalgoritmen met hun controller, processor, of een middelingsengine op de chip die verschillende convertorsamples vastlegt. Het middelingsproces "egaliseert" de conversiegroep en verbetert de effectieve resolutie door systeemruisonderdrukking.

Voor de uitvoering van het afvlakken van de geconverteerde gegevens moeten meerdere signaalacquisities met een constante samplesnelheid worden uitgevoerd en moet het gemiddelde worden genomen van een vooraf bepaald aantal monsters. Het proces van middeling is welbekend. De som van de ADC-resultaten (opeenvolgende samples, x) gedeeld door het aantal monsters (N) levert een gemiddelde waarde op (Vergelijking 1).

 Vergelijking 1

Dit proces vermindert de uitgangsdatasnelheid met een factor N, maar verhoogt de bezinkingstijd van het systeem.

De standaardafwijking van de gemiddelde ruismonsters (σ_avg) is de standaardafwijking van het oorspronkelijke signaal (σ_sig) gedeeld door de vierkantswortel van N (Vergelijking 2).

 Vergelijking 2

De opeenvolgende monsters, met inbegrip van ongecorreleerde ruis, zullen resulteren in meer ruisonderdrukking bij een constant signaalgemiddelde. Elk opeenvolgend gemiddeld monster leidt tot een verbetering van de signaal-ruisverhouding (SNR) indien het signaal gelijkstroom is en de ruiscomponent willekeurig is.

De SNR-verbetering is evenredig met de vierkantswortel van het aantal gemiddelde monsters. Een gemiddelde van vier DC-signaalmonsters (4¹) verhoogt de effectieve resolutie van de omzetter met één met een toename van 6 decibel (dB) in de SNR. Een gemiddelde van 16, of4², monsters verhoogt de effectieve resolutie met twee en de SNR met 12 dB. Met deze logica zal een groepsgrootte van 4^N het aantal effectieve bits van een omzetting met N doen toenemen, waardoor de systeemruis tot nul en de SNR-waarde tot oneindig wordt gebracht.

De Allan-variantie

Een SNR-waarde gelijk aan oneindig is natuurlijk absurd. In de echte wereld neemt de verwerving van het benodigde aantal monsters tijd in beslag, gedurende welke het systeem kan veranderen in termen van driftgraden.

De Allan-variantie, bekend als twee-monsters-variantie, meet de frequentiestabiliteit in klokken, oscillators, ADC's en versterkers door de verandering in ruis weer te geven als het aantal monsters dat wordt gebruikt voor de middeling van een signaal, wordt verhoogd. Het statistische analyse-instrument Allan variance bepaalt het maximum aantal vereiste monsters dat optimaal zal zijn voor een bepaald systeem, waarbij de stabiliteit wordt ingeschat door te wijzen op frequentiedrift of temperatuureffecten.

Zo kunnen de gegevens in een systeem van een ADC in de loop van de tijd verschuivingen vertonen, zoals te zien is in Afbeelding 3.

Afbeelding 3: De 30.000 ADC-uitgangsdatapunten die gedurende negen minuten zijn opgenomen, vertonen een lichte drift in de gegevens over die periode, waardoor de berekening van de Allan-variantie verslechtert. (Afbeelding bron: Electronic Design)

Het variantie-algoritme neemt meerdere reeksen van steeds langere gemiddelden en beoordeelt de resulterende ruis van elke reeks (Afbeelding 4).

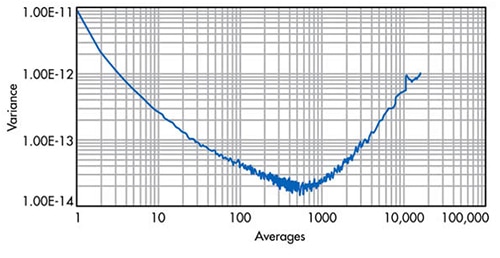Afbeelding 4: Toegepaste Allan-variantieberekening voor de gegevenspunten in Afbeelding 3. Bij een gemiddelde van 500 punten krijgt dit ADC-systeem 4,48 bits of een SNR-verhoging van 27 dB. (Afbeelding bron: Electronic Design)

Afbeelding 4 toont aan dat de minimale variantie van de datapunten van dit specifieke systeem optreedt bij ongeveer 500 ADC-uitgangsgemiddelden - het optimale aantal monstergemiddelden voor de beperking van ruis. Bij een gemiddelde van 500 punten verwerft dit ADC-systeem 4,48 bits of een SNR-verhoging van 27 dB. Voor en na het 500e gemiddelde punt verslechteren de resultaten in Afbeelding 4, omdat de gegevensdrift een grotere factor wordt. Variabelen die van invloed zijn op de Allan-variantieberekeningen kunnen zijn: tijd, signaalstabiliteit, drift, variaties in de voeding en veroudering van het product. Indien een digitaal middelingsfilter wordt gebruikt, is het verstandig het systeem als geheel te evalueren met het Allan-variantie-instrument.

Real-world oplossing

SAR-convertors kunnen programmeerbare versterker- (PGA) en digitale filterfuncties bieden om de effectieve resolutie en LSB-spanning (least significant bit) te verhogen. Zo is de AD7606C-18 van Analog Devices een A/D data-acquisitiesysteem (DAS) met 18 bits, 1 MSPS simultane bemonstering, acht kanalen, elk met analoge ingangsklembeveiliging, een PGA, een LPF, en een 18-bit SAR ADC.

Het apparaat heeft ook analoge ingangsbuffers met een ingangsimpedantie van 1 mega-ohm (MW) en programmeerbare true bipolaire differentiële, bipolaire single-ended, en unipolaire single-ended ingangsspanningsconfiguraties. De AD7606C-18 maakt de aansluiting mogelijk van acht verschillende onafhankelijke ingangssensors of signaalkanalen.

Het digitale filter van de AD7606C-18 heeft een overbemonsteringsfunctie die het gemiddelde neemt van repeterende samples van 1 tot 256 (4⁴). Volgens het Allan variantie-instrument verbetert deze overbemonsteringsfunctie de ruisprestaties aan de digitale uitgang van de convertor. De ADR4525 lage ruis, 2,5 volt precisie spanningsreferentie vult het AD7606C-18 DAS systeem aan met een 1 deel per miljoen per graad Celsius (ppm/°C) maximale temperatuur coëfficiënt en 1 microvolt (mV) piek-tot-piek typische uitgangsruis (Afbeelding 5).

Afbeelding 5: De AD7606C-18 SAR-ADC met de ADR4525 2,5 volt precisie spanningsreferentie. De spoelen met LPF's van de eerste orde op de ingangskanalen V1 tot en met V8 bemonsteren gelijktijdig alle acht kanalen. (Bron afbeelding: Analog Devices)

Zoals Afbeelding 5 laat zien, kan dit type SAR-array met hoge ingangsimpedantie rechtstreeks communiceren met sensors zonder de typische externe stuurversterkers. Een externe sensorversterkingstrap kan ook overbodig zijn. Tegelijkertijd heeft de SAR-convertor een interne PGA- en LPF-fase die voor signaalverwerking zorgt, gevolgd door een digitaal filter met middeling om de ruis verder te verminderen door hogere effectieve resoluties te bieden. Een dergelijke DAS kan een effectieve resolutie van 17,1 bit bieden met een conversiesnelheid van 3,9 kilomonsters per seconde (ksps). Aan de andere kant van het conversiesnelheidspectrum biedt dit toestel een 15 bits effectieve resolutie met een conversiesnelheid van 1 MSPS.

De snelste conversiesnelheid van de AD7606C-18 is 1 MSPS met overbemonstering gelijk aan één. Als de kanaaloverbemonstering van de convertor twee is, of het gemiddelde van de monsters van een kanaal twee keer, is de conversiesnelheid de helft van de maximale conversiesnelheid bij 500 ksps. Voor overbemonstering gelijk aan vier, of 4¹ als het aantal monsters gemiddeld is, is de conversiesnelheid van dat kanaal 250 ksps, enzovoort. Voor elk van de acht kanalen levert het systeem met een overbemonsteringswaarde van 256 een ±10 volt single-ended bereik, 17,1 bit effectieve resolutie (105 dB SNR), met een conversiesnelheid van 3,9 ksps (Tabel 1).

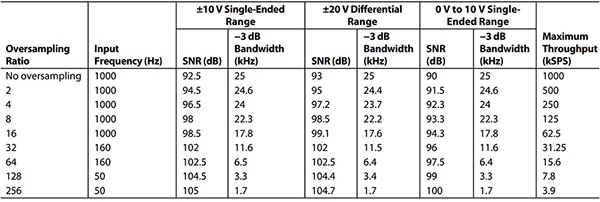Tabel 1: Overbemonsteringprestaties, lage bandbreedte modus van de AD7606C-18. (Bron: Analog Devices)

De formule voor de omrekening van SNR naar effectieve resolutie (effectief aantal bits, of ENOB) is weergegeven in vergelijking 3.

Vergelijking 3

Aan het andere eind van het conversiesnelheidspectrum biedt dit toestel, met een overbemonsteringsfactor van 1, een effectieve resolutie van 15 bits (92,5 dB SNR) met een conversiesnelheid van 1 MSPS (tabel 1).

Er zijn nog meer verbeteringen die de AD7606C-18 biedt. Aangezien er acht afzonderlijke SAR ADC's op de chip zijn, hebben alle acht kanalen een gelijktijdige bemonsteringsfunctie. Met deze functie is het mogelijk het digitale filter te implementeren om gelijktijdig op alle kanalen een hoge resolutie of hoge snelheid te bereiken. Bovendien kunnen alle kanalen worden gekalibreerd en gediagnosticeerd.

De systeemfase-kalibratie van de AD7606C-18 detecteert bijvoorbeeld de misaanpassing van het discrete ingangsfilter. Deze waardevolle functie identificeert elke mismatch op de discrete componenten of in de gebruikte sensor die fasemismatch kan veroorzaken tussen gelijktijdig bemonsterde kanalen. De softwaremodus van het apparaat compenseert de fasemismatch per kanaal door het bemonsteringstijdstip van een afzonderlijk kanaal te vertragen.

De kalibratie van de systeemversterking detecteert de weerstandsmismatches van het discrete ingangsfilter. Deze mogelijkheid helpt om externe weerstandsverschillen te overbruggen. De softwaremodus compenseert de versterkingsfout per kanaal door de gebruikte waarde van de serieweerstand in het corresponderende register te schrijven.

De offsetkalibratie van het systeem houdt rekening met de offsets van het ingangssignaal tijdens de kalibratieactiviteit. De software kan de offset van de externe sensor van elk kanaal of de mismatch van elk extern weerstandspaar aanpassen.

Voor een specifieke toepassing heeft de EVAL-AD7606SDZ kaart voor de AD7606 software om te helpen bij apparaatevaluaties met apparaatprogrammering, alsmede golfvorm-, histogram-, en FFT-opname (figuur 6).

Afbeelding 6: Het AD7606-evaluatiebord (links) aangesloten op het SDP-bord (System Demonstration Platform) (rechts), waarmee het evaluatiebord kan worden bediend via de USB-poort van een PC. (Bron afbeelding: Analog Devices)

Met de software van de evaluatiekaart kan de gebruiker de overbemonsteringswaarde van elk kanaal, het ingangsbereik, het aantal monsters en de actieve kanaalselectie configureren. Bovendien maakt deze software het ook mogelijk om testgegevensbestanden op te slaan en te openen.

Conclusie

Ondanks een verschuiving naar digitaal, is het nog steeds een analoge wereld en ontwerpers hebben analoge-centrische elektronica nodig om hoge-resolutie, hoge-snelheid conversieproblemen op te lossen. Zoals blijkt, verbetert de eenvoudige combinatie van een analoge LPF en een digitaal middelingsfilter, geïmplementeerd met het juiste aantal gemiddelden, de prestaties van een 1 MSPS SAR-convertor aanzienlijk.