Hoe pas je de Wet van Ohm toe op serie- en parallelschakelingen

Laten we beginnen met uitzoeken wat de wet van Ohm eigenlijk is en hoe hij wordt toegepast op wat we vandaag bespreken. De Wet van Ohm is vernoemd naar Georg Ohm. Hij ontdekte dat de stroom die door een geleider stroomt direct samenhangt met de spanning en de weerstand. Dit betekent dat de spanning kan worden gevonden door de stroom en de weerstand in een schakeling of component te vermenigvuldigen.

Voorbeelden: V=I x R, R=V/I, I=V/R

Waarbij:
V = Voltage (spanning)
I = Current (stroom)
R = Resistance (weerstand)

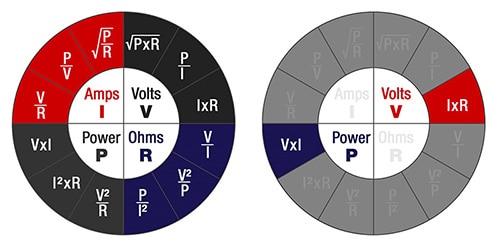
Hoe kunnen we dit toepassen op een schakeling? Eerst moeten we ontcijferen of het een serie- of parallelschakeling is, omdat die ieder hun eigen regels hebben om tot een totaal te komen voor iedere waarde. De vergelijkingen van serieschakelingen zijn als volgt (C hieronder staat voor capaciteit):

V_T= V₁+V₂+...

I_T= I₁= I₂= ...

R_T= R₁+R₂+...

1/C_T= 1/C₁+1/C₂+...

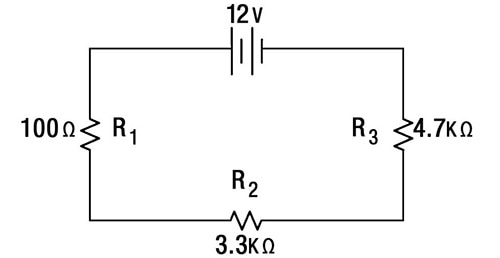
Ok, op de onderstaande afbeelding is een serieschakeling te zien waarvan maar enkele waarden gegeven zijn. Met de bovenstaande serievergelijkingen, in combinatie met de wet van Ohm, kunnen we alle waarden oplossen.

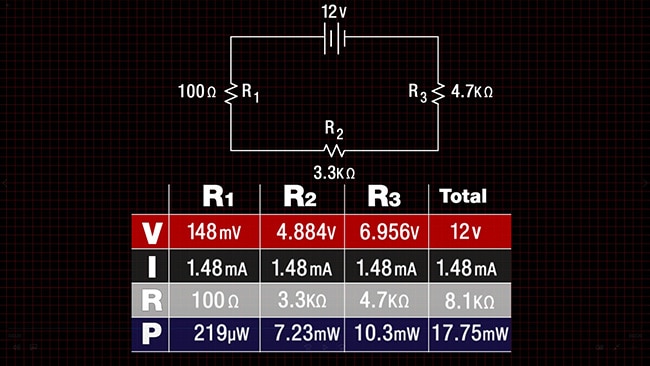
Op de volgende afbeelding staat de tabel met alle correcte waarden erin. Begin met het optellen van de weerstand, om het totaal van 8,1 KΩ te krijgen. Omdat we ook de totale spanning weten van 12 V, kunnen we als volgt het stroomtotaal berekenen: (12 V)/(8100 Ω) = 0,00148 A of 1,48 mA. Deze stroom is hetzelfde in de hele schakeling omdat alles in serie staat. Nu we alle stroomwaarden en alle weerstandswaarden weten, kunnen we alle spanningstotalen uitrekenen met V=I x R. Om het vermogen (P, power) te berekenen, gebruik je P=I x V. Zo simpel is het.

Nu bespreken we de vergelijkingen voor een parallelschakeling:

V_T= V₁=V₂=...

I_T= I₁+I₂+...

1/R_T= 1/R₁+1/R₂+...

C_T= C₁+C₂+...

Wat is er veranderd? In een parallelschakeling is de totale spanning gelijk aan de spanning in iedere tak van de parallelschakeling. De stroom wordt opgeteld om het totaal te vinden. De vergelijkingen voor weerstand en capaciteit zijn omgekeerd.

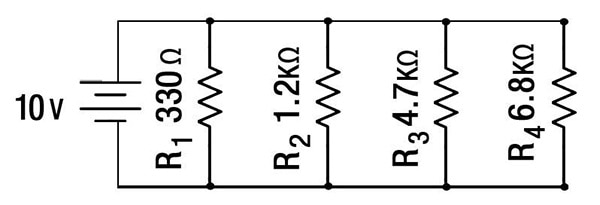
Hieronder staat de weergave van een parallelschakeling met enkele gegeven waarden. Met de bovenstaande parallelvergelijkingen, in combinatie met de wet van Ohm, kunnen we alle waarden oplossen.

De onderstaande afbeelding is een tabel met alle correcte waarden erin. Tot nu toe weten we dat de spanning 10 V is, dus dat hebben we overal ingevuld. Nu kunnen we de totale weerstand als volgt berekenen: 1/(330 Ω)+1/(1200 Ω)+1/(4700 Ω)+1/(6800 Ω) = 0,0042234/Ω. Dan nemen we het omgekeerde van dat totaal en krijgen we 236,96 Ω. Om de rest van de waarden in te vullen, kunnen we de wet van Ohm gebruiken. Met I=V/R krijgen we alle spanningstotalen. Gebruik daarna weer P=I x V voor de vermogenswaarden.

Je hebt vast gemerkt dat we niet alle serie- en parallelvergelijkingen hebben gebruikt, maar in plaats daarvan voor sommige de wet van Ohm hebben toegepast. Ze kunnen in combinatie worden gebruikt om te controleren of het eerste antwoord juist is. Deze vergelijkingen zijn relevant bij het plannen van een schakeling, dus is het van groot belang om ze te leren als je met elektronica aan de slag wilt. Maar maak je geen zorgen, DigiKey heeft een paar online calculators die daarbij kunnen helpen. Oefening baart kunst. Veel plezier met leren!